系统的无源性
术语
Passivity的字面翻译是「被动性」,但在各个领域中通常都翻译为「无源性」,因为这一术语与物理系统中能量传递和消耗的特性有关。Passivity描述系统不会产生能量而只能存储或消耗能量的特性。
定义
无记忆系统模型
对于由方程\(y=h(t,u)\)描述的无记忆系统,无源性的定义如下:

无源性可以通过分析\(u-y\)曲线在象限中的分布来判断,即通过确定\(u^T y\)的符号来实现。此外,\(u^T y\)满足的某些不等式关系可以用其所属的扇区(sector)从几何角度加以描述:
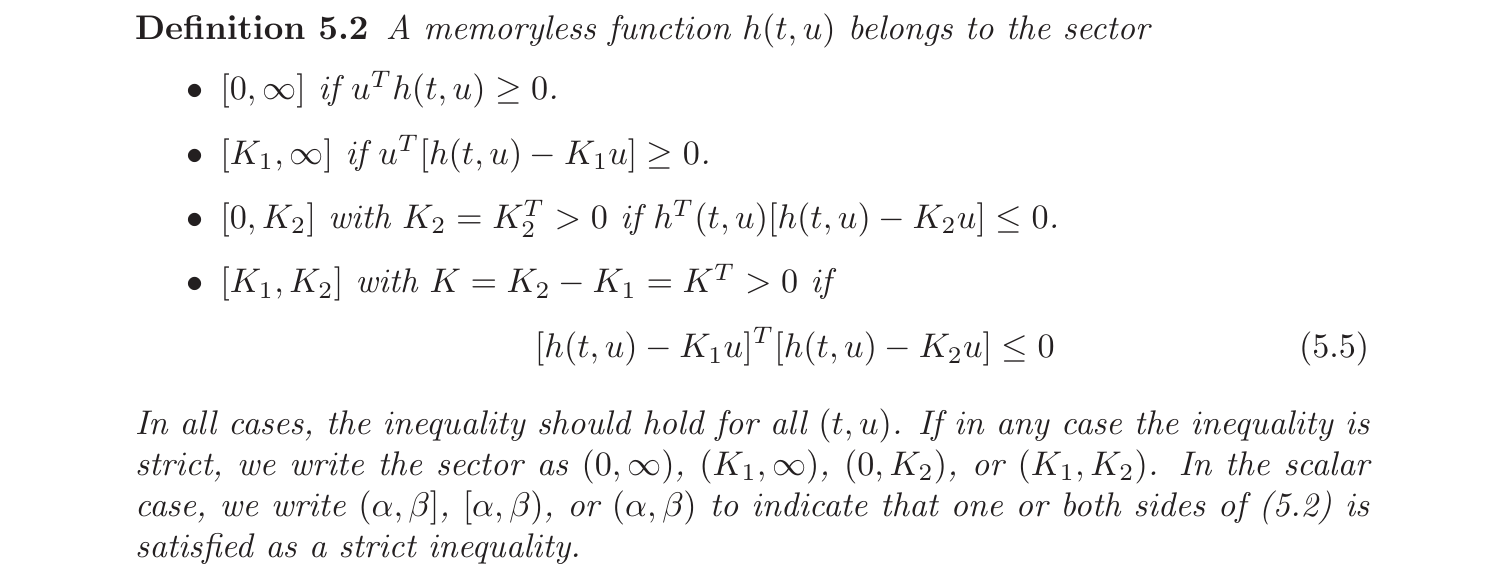
状态空间模型
对于如下由状态方程描述的动态系统: \[ \dot{x}=f(x,u),\,\,y=h(x,u) \]
其中\(u\)是系统输入,\(y\)是系统输出,\(f\)是局部Lipschitz函数,\(h\)是连续函数,且有\(f(0,0)=0\)以及\(h(0,0)=0\),说明状态\(x\)和输入\(u\)均为\(0\)时,系统处于平衡状态且系统输出为零。动态系统无源性的定义如下:

简单来说,无源性条件说明系统吸收的能量(即输入功率\(u^Ty\))不小于系统所存储能量的变化率(即存储函数\(V(x)\)的导数\(\dot{V}\)),这意味着系统不会产生能量,能量只会消耗或储存。
稳定性
对于前面的动态系统,原点是\(\dot{x}=f(x,0)\)的一个平衡点,现在分析原点的稳定性。根据无源性定义中那熟悉的记号和公式,很容易将它与系统稳定性联系到一起。
将定义中的存储函数定义为Lyapunov函数,很容易证明,若无源系统存在正定的存储函数,则它一定是稳定的:

渐进稳定性条件则更加复杂一些:

总结
通过上面的讨论可知,无源性与系统的能量传递密切相关。无源系统如果不产生能量,任何从外部输入吸收的能量要么被存储,要么消散。许多物理系统本身就是无源的,例如电路中的电阻和机械系统中的摩擦力,它们都会消耗能量。无源性常用作分析稳定性的工具。无源系统具有良好的稳定性特性,例如,无源系统的反馈互连在某些条件下是稳定的(称为「无源性定理」)。
对于线性时不变系统,可以通过传递函数的特性来检查无源性。具体来说,如果系统是无源的,则传递函数\(H(s)\)要满足某些条件,比如正实性(positive real),这意味着\(H(s)\)有实数的极点和零点,且\(H(j\omega)\)的实部对于所有频率\(\omega\)都是非负的。