反馈系统的稳定性
简介
负反馈是控制系统的灵魂。它使系统能够自动调节自身,实现更高的精确度和稳定性,抵抗外部扰动和不确定因素。但反馈也可能引发问题,比如,两个稳定系统通过反馈连接后,整体系统可能变得不稳定。
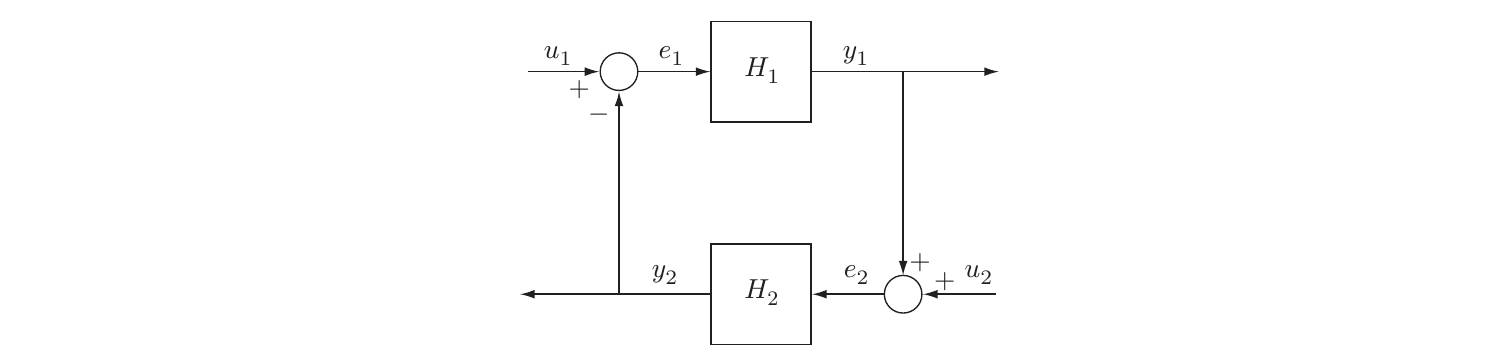
本文首先介绍了无源性定理和小增益定理,它们是Nyquist稳定性判据在非线性系统中的扩展。随后,将系统建模为前向通道为线性时不变模型、反馈通道为无记忆的非线性模型,利用绝对稳定性的理论,通过圆判据和Popov判据来分析系统的稳定性。
无源性定理
无源性定理中最基本的结论是:两个无源系统的反馈连接是无源的(The feedback connection of two passive systems is passive)。接着便可以利用无源性去研究反馈系统的稳定性和渐进稳定性,本文不再介绍。
小增益定理
小增益定理(small-gain theorem)叙述如下:

图1中的反馈连接为研究反馈系统的鲁棒性(robustness)问题提供了一个方便的方法。面对模型不确定性的反馈系统,可以表示为一种反馈连接,其中\(H_1\)是稳定的名义系统(nominal system),\(H_2\)是稳定的扰动系统。当\(\gamma_2\)足够小时,就能满足条件\(\gamma_1\gamma_2<1\)。因此,小增益定理为理解反馈系统中的许多鲁棒性结果提供了一个概念框架。
绝对稳定性
定义
对于如下特征的系统:
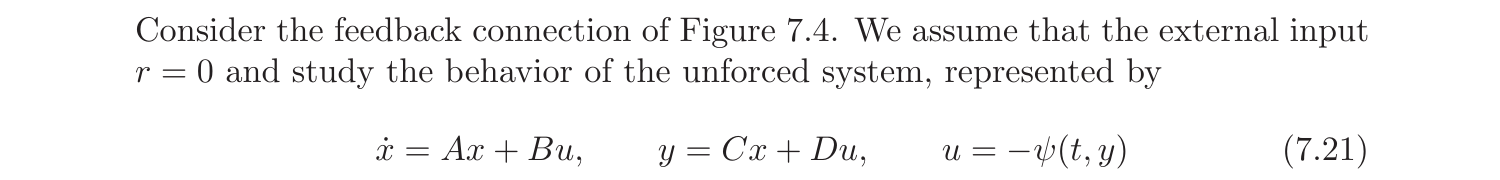

所研究对象的结构框图如上图所示,它是本文开头所述一般反馈结构的一个特例。前向通道中的\(G(s)\)是一个线性时不变系统,模型可以用传递函数阵表示。而反馈通道的\(\psi(\cdot)\)则是一个无记忆系统,可能是时变和非线性的。绝对稳定性研究的是当\(\psi\)满足扇区条件时,原点的全局一致渐进稳定性(globally uniformly asymptotically stable, GUAS),其定义如下:

回顾全局一致渐进稳定性的特征:全局表示从任何初始条件出发,系统状态总是收敛到平衡点;一致表示存在一个统一的收敛速率,对所有初始状态都适用;渐进稳定表示状态随着时间无限趋向于平衡点。接下来介绍两个稳定性判据。
圆判据
圆判据(circle criterion)要用到扇区条件的定义,详见系统的无源性。圆判据的第一个结论针对多输入多输出系统,也称为多变量圆判据:

对于单输出系统,即\(m=1\)时,可以通过\(G(s)\)的Nyquist图来验证。对于\(\psi\in[\alpha,\beta],\beta>\alpha\),如果传递函数 \[ Z(s)=\frac{1+\beta G(s)}{1+\alpha G(s)} \tag{1} \] 是严格正实函数,则系统绝对稳定。\(Z(s)\)是严格正实的如果它是Hurwitz而且 \[ \mathrm{Re}\left[\frac{1+\beta G(j\omega)}{1+\alpha G(j\omega)}\right]>0,\,\forall\,\omega\in[0,\infty] \tag{2} \]
对于单输出系统,即\(m=1\)的情况,可以通过\(G(s)\)的Nyquist图进行验证。对于\(\psi\in[\alpha,\beta]\)且\(\beta>\alpha\),如果传递函数 \[ Z(s)=\frac{1+\beta G(s)}{1+\alpha G(s)} \tag{3} \] 是严格正实函数,则系统是绝对稳定的。传递函数\(Z(s)\)被称为严格正实函数,当且仅当它是Hurwitz稳定的,并且满足以下条件: \[ \mathrm{Re}\left[\frac{1+\beta G(j\omega)}{1+\alpha G(j\omega)}\right]>0,\,\forall\,\omega\in[0,\infty] \tag{4} \]
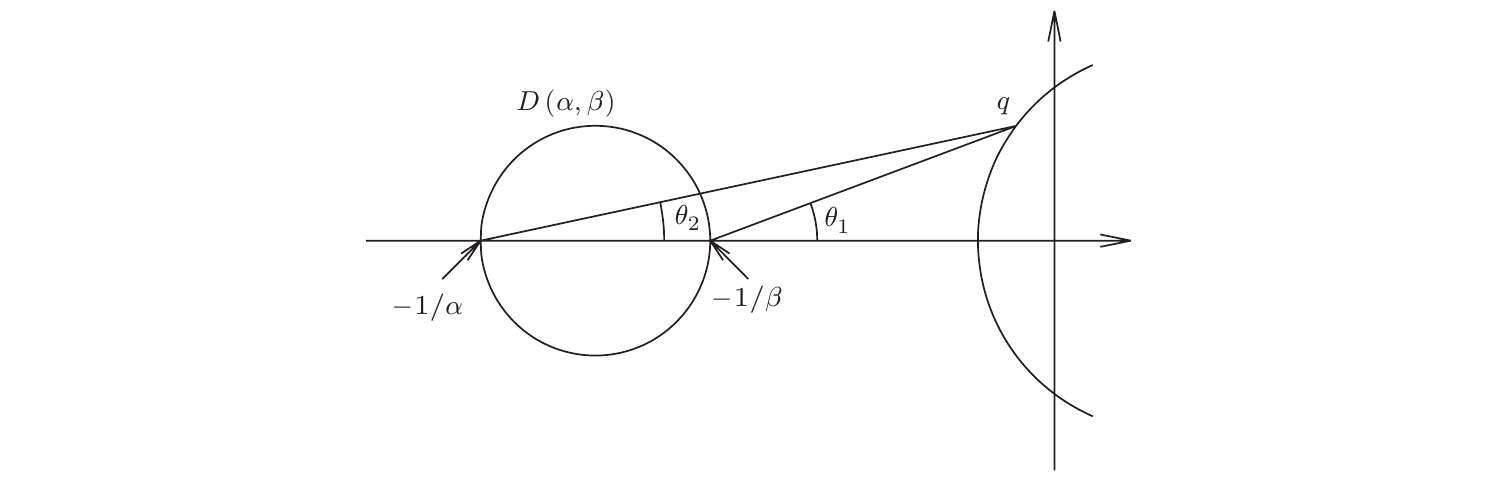
当\(\alpha>0\)时,上面的表达式可以写作 \[ \mathrm{Re}\left[\frac{1/\beta+G(j\omega)}{1/\alpha+G(j\omega)}\right]>0,\,\forall\,\omega\in[0,\infty] \tag{5} \]
对于Nyquist图上的一点\(q\),两个复数\(1/\beta+G(j\omega)\)和\(1/\alpha+G(j\omega)\)可以分别表示为从\(q\)到\(-1/\beta+j0\)和\(-1/\alpha+j0\)的连线。当两个复数之间的角度差小于\(\pi/2\)时,它们的比值的实部是正的,也就是上图中的\((\theta_1-\theta_2)<\pi/2\)。定义\(D(\alpha,\beta)\)为如图所示的闭合圆盘,容易发现,当\(q\)在圆盘外部时\((\theta_1-\theta_2)<\pi/2\)成立。由于上述条件对所有的\(\omega\)都成立,所以\(G(s)\)的Nyquist图上所有的点必须严格位于圆盘之外。另一方面,若\(G(s)/[1+\alpha G(s)]\)是Hurwitz稳定的,则\(Z(s)\)是Hurwitz稳定的。根据Nyquist判据,当且仅当\(G(s)\)的Nyquist图不与点\(-1/\alpha+j0\)相交,并且以逆时针方向绕该点恰好\(p\)圈时,\(G(s)/[1+\alpha G(s)]\)是Hurwitz稳定的,其中\(p\)是\(G(s)\)在复数平面的开右半平面内的极点数量。因此,当\(G(s)\)的Nyquist图不进入圆盘\(D(\alpha,\beta)\)并以逆时针方向绕其\(p\)圈时,定理\(7.8\)的条件得到满足。
接下来,考虑\(\beta>0\)且\(\alpha=0\)的情况。对于这种情况,定理\(7.8\)要求\(1+\beta G(s)\)为严格正实。这种情况成立的条件是\(G(s)\)是Hurwitz稳定的,并且 \[ \mathrm{Re}[1+\beta G(j\omega)]>0\quad\Longleftrightarrow\quad\mathrm{Re}[G(j\omega)]>-\frac{1}{\beta}, \,\forall\, \omega\in[0,\infty] \] 这等价于图形条件,即\(G(s)\)的Nyquist图位于由\(\mathrm{Re}[s]=-1/\beta\)定义的垂直线的右侧。
最后,考虑\(\alpha<0<\beta\)的情况,此时\((4)\)等价于 \[ \mathrm{Re}\left[\frac{1/\beta+G(j\omega)}{1/\alpha+G(j\omega)}\right]<0, \,\forall\, \omega\in[0,\infty] \tag{6} \] 不等号的方向反转是因为在从\((4)\)到\((6)\)的过程中乘上了\(\alpha/\beta\),而这个值现在是负的。重复之前的论证可以看到,要使\((6)\)成立,\(G(s)\)的Nyquist图必须位于圆盘\(D(\alpha,\beta)\)内。因此,Nyquist图不能环绕点\(-1/\alpha+j0\)。因此,根据Nyquist判据可知,为了使\(G(s)/[1+\alpha G(s)]\)稳定,\(G(s)\)必须是Hurwitz稳定的。
这三种情况下的稳定性判据总结在以下定理中,该定理被称为圆判据。

圆判据使我们能够仅通过使用\(G(s)\)的Nyquist图来研究绝对稳定性,而Nyquist图可以直接从实验数据中确定。根据\(G(s)\)的Nyquist图,我们可以确定系统绝对稳定的允许区间。
Popov判据
Popov判据针对下面这类系统:

其中,\(\psi\)是时变而且解耦的,即\(\psi_i(y)=\psi_i(y_i)\)。Popov判据的内容如下:
