CPA安全方案的构建与安全性证明

发表于 2022-11-25 分类于大学课程 Waline：本文字数： 2.9k 阅读时长 ≈ 10 分钟

安全性定义

选择明文攻击（Chosen-Plaintext Attack）指敌手能够选择不同的明文作为输入提供给加密算法，得到相应的密文，以此确定其他密文对应的明文，从而破解方案。

攻击过程可形式化为，允许敌手\(\mathcal{A}\)和加密预言机（encryption oracle）自由交互，\(\mathcal{A}\)访问预言机\(\mathcal{O}\)的过程记为\(\mathcal{A}^{\mathcal{O}(\cdot)}\)，如果\(\mathcal{O}\)是加密算法\(\mathsf{Enc}_k\)，则记为\(\mathcal{A}^{\mathsf{Enc}_k(\cdot)}\)。\(\mathcal{A}\)提供明文消息\(m\)作为输入，预言机返回密文\(c\gets\mathsf{Enc}_k(m)\)作为回复，这便是一次询问过程。安全性的定义要求：即使\(\mathcal{A}\)能访问加密预言机，也无法区分两条任意消息的密文。

对称密钥加密方案\(\Pi=(\mathsf{Gen},\mathsf{Enc},\mathsf{Dec})\)，CPA不可区分实验记作\(\mathsf{PrivK}_{\mathcal{A},\Pi}^{\mathsf{cpa}}(n)\)，定义如下：

生成密钥\(k\gets\mathsf{Gen}(1^n)\)
\(\mathcal{A}\)能访问预言机\(\mathsf{Enc}_k(\cdot)\)，输入\(1^n\)给\(\mathcal{A}\)，\(\mathcal{A}\)输出一对长度相等的消息\(m_0\)和\(m_1\)
选择随机比特\(b\gets\{0,1\}\)，计算出密文\(c\gets\mathsf{Enc}_k(m_b)\)交给\(\mathcal{A}\)，\(c\)称为挑战密文
\(\mathcal{A}\)继续访问预言机，输出一个比特\(b'\)
如果\(b=b'\)，则该实验输出\(1\)，否则输出\(0\)

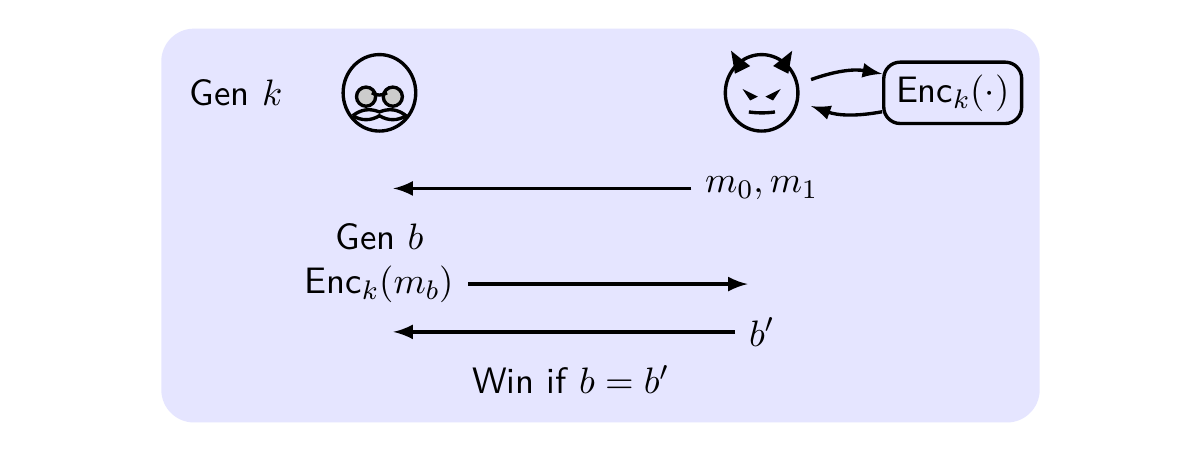
定义描述了敌手\(\mathcal{A}\)利用预言机\(\mathsf{Enc}_k(\cdot)\)攻击方案\(\Pi\)的过程，当\(\mathsf{PrivK}_{\mathcal{A},\Pi}^{\mathsf{cpa}}(n)=1\)时，\(\mathcal{A}\)成功攻破方案。如果对任意概率多项式敌手\(\mathcal{A}\)，存在可忽略函数\(\mathsf{negl}\)，使得 \[ \mathrm{Pr} \Big[\mathsf{PrivK}_{\mathcal{A},\Pi}^{\mathsf{cpa}}(n)=1\Big] \le \frac{1}{2} + \mathsf{negl}(n) \tag{1} \]

则方案是选择明文攻击条件下的不可区分加密，或者说是CPA安全的。

伪随机函数

从密码学中的归约证明过程一文可知，伪随机数发生器能够保证窃听者存在时的安全性，伪随机函数（pseudorandom function）则可以用来构造CPA安全的加密方案。

现研究将\(n\)长度字符串映射到另一个\(n\)长度字符串的伪随机函数。带密钥的函数\(F\)是双输入函数： \[ F:\{0,1\}^* \times \{0,1\}^* \to \{0,1\}^* \]

第一个输入为密钥\(k\)，第二个输入才是输入。一般来说，密钥\(k\)一旦选择好就固定了，于是考虑单输入函数： \[ F_k:\{0,1\}^* \to \{0,1\}^* \] \[ F_k(x) \overset{\mathrm{def}}{=} F(k,x) \]

通常假设\(F\)是定长的，即密钥\(k\)、输入\(x\)和函数值\(F_k(x)\)的长度相同。那么伪随机函数\(F_k(\cdot)\)通过固定密钥\(k\in\{0,1\}^{n}\)将\(n\)长度的字符串映射到另一个\(n\)长度的字符串。每个密钥对应一种函数分布，所以\(F_k\)最多可从\(2^n\)个不同的函数分布中选择。

考虑所有将\(n\)长度字符串映射到\(n\)长度字符串的函数，它们构成的集合记作\(\mathsf{Func}_n\)，将函数看成查找表（look-up table），可得集合的大小为\(2^{n\cdot 2^n}\)。从中均匀随机选择一个函数\(f\in\mathsf{Func}_n\)，那么\(f\)是「真正的」随机函数。

如果对所有的多项式时间区分器\(D\)，存在可忽略函数\(\mathsf{negl}\)，满足 \[ \left| \mathrm{Pr} \big[ D^{F_k(\cdot)}(1^n)=1 \big] - \mathrm{Pr} \big[ D^{f(\cdot)}(1^n)=1 \big] \right| \le \mathsf{negl}(n) \tag{2} \]

则称\(F\)是伪随机函数，其中\(k\gets\{0,1\}^n\)是均匀随机选择的，\(f\)是从所有将\(n\)长度字符串映射到\(n\)长度字符串的函数集合\(\mathsf{Func}_n\)中均匀随机选择的。前者是从\(2^n\)个不同的函数分布中选择出来的，后者是从\(2^{n\cdot 2^n}\)个不同的函数分布中选择出来的，但任意区分器都无法在多项式时间内区分到底是在和\(F_k\)还是\(f\)交互。

基于伪随机函数构建CPA安全的加密方案，方案安全性证明的关键点在于，如果敌手能够攻破该方案，则它能将伪随机函数和真正的随机函数区分开来。我们能在后面的归约证明过程中看到这一点。

方案构建

令\(F\)是伪随机函数，定义消息长度为\(n\)的对称密钥加密方案\(\Pi=(\mathsf{Gen},\mathsf{Enc},\mathsf{Dec})\)如下：

\(\mathsf{Gen}\)：输入\(1^n\)，均匀随机选择密钥\(k\gets\{0,1\}^n\)
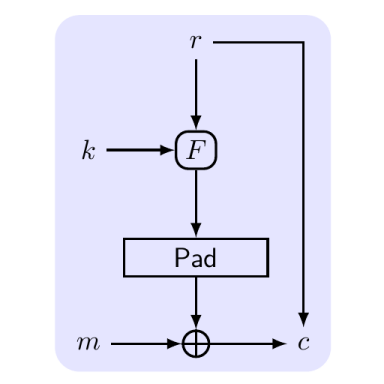
\(\mathsf{Enc}\)：输入密钥\(k\in\{0,1\}^n\)，以及消息\(m\in\{0,1\}^n\)，均匀随机选择\(r\gets\{0,1\}^n\)，输出密文 \[ c:=\left \langle r, F_k(r) \oplus m_b \right \rangle \]
\(\mathsf{Dec}\)：输入密钥\(k\in\{0,1\}^n\)，以及密文\(c=\left \langle r, s \right \rangle\)，输出明文消息 \[ m:=F_k(r)\oplus s \]

简单定义\(\mathsf{Enc}_k(m)=F_k(m)\)是不可行的，因为\(\mathsf{Enc}_k(\cdot)=F_k(\cdot)\)是确定函数（deterministic function），给定相同的输入一定会得到相同的输出。敌手经过多次实验尝试，总能找到某个明文对应的密文与挑战密文相同，从而破解方案。任何CPA安全的加密方案必须是概率的（probabilistic），随机性必须是加密过程的一部分，以保证相同的明文得到不同的密文。

该构造方案是概率的，通过伪随机函数将随机值\(r\)映射到另一个字符串，然后将字符串与明文异或，得到密文。\(F_k(r)\)对于观察密文\(\left\langle r,s \right\rangle\)的敌手来说，看上去是完全随机的。因此，该加密方案和「一次一密」非常相似，只要\(r\)没有在之前某次加密中使用过。

安全性证明

攻破方案的概率

将加密方案\(\Pi\)中的伪随机函数\(F_k\)替换成随机函数\(f\gets\mathsf{Func}_n\)，得到的加密方案记为\(\widetilde{\Pi}=(\widetilde{\mathsf{Gen}},\widetilde{\mathsf{Enc}},\widetilde{\mathsf{Dec}})\)。除了真正的随机函数\(f\)取代了\(F_k\)之外，\(\widetilde{\Pi}\)与\(\Pi\)完全相同。敌手\(\mathcal{A}\)最多向加密预言机询问\(q(n)\)次，其中\(q(\cdot)\)是多项式。那么\(\mathcal{A}\)攻破\(\widetilde{\Pi}\)的概率 \[ \mathrm{Pr} \Big[ \mathsf{PrivK}_{\mathcal{A},\widetilde{\Pi}}^{\mathsf{cpa}}(n)=1 \Big] \le \frac{1}{2}+\frac{q(n)}{2^n} \tag{3} \]

下面分析如何得到\((3)\)的结果。

令\(r_c\)为生成挑战密文\(c=\left\langle r_c,f(r_c) \oplus m_b \right\rangle\)时用到的随机值。\(\mathcal{A}\)向加密预言机询问\(q(n)\)次可得到\(\{\left\langle r_i,f(r_i) \right\rangle\}\)，因为返回给\(\mathcal{A}\)的密文\(c_i=\left\langle r_i,s_i \right\rangle\)，\(f(r_i)=s_i\oplus m_i\)，其中\(i=1,\dots,q(n)\)。根据随机值\(r_c\)是否被重复使用，分两种情况讨论：

加密预言机在回答\(\mathcal{A}\)的询问时至少用到过一次\(r_c\)，记作事件\(\mathsf{Repeat}\)。这种情况下\(\mathcal{A}\)能轻易判断出哪条消息被加密，只需根据询问预言机得到的\(\left\langle r_c,f(r_c) \right\rangle\)计算\(m_0\)和\(m_1\)对应的密文，其中必有一条与挑战密文\(c\)相同。\(r_c\in\{r_i\}\)的概率最多为\(q(n)/2^n\)，所以该事件发生的概率最多为\(q(n)/2^n\)。
加密预言机在回答\(\mathcal{A}\)的询问时从未用到过\(r_c\)，记作事件\(\lnot\mathsf{Repeat}\)。那么\(\mathcal{A}\)和加密预言机的交互过程中没有掌握任何关于\(f(r_c)\)的信息，这意味着\(f(r_c)\)和\(m_b\)做异或后的值完全随机（与「一次一密」类似），所以\(\mathcal{A}\)输出\(b'=b\)的概率是\(1/2\)。

综合这两种情况，可得\(\mathcal{A}\)攻破\(\widetilde\Pi\)的概率 \[ \begin{align} \mathrm{Pr} \Big[ \mathsf{PrivK}_{\mathcal{A},\widetilde{\Pi}}^{\mathsf{cpa}}(n)=1 \Big] & = \mathrm{Pr} \Big[ \mathsf{PrivK}_{\mathcal{A},\widetilde{\Pi}}^{\mathsf{cpa}}(n)=1 \wedge \mathsf{Repeat} \Big] + \mathrm{Pr} \Big[ \mathsf{PrivK}_{\mathcal{A},\widetilde{\Pi}}^{\mathsf{cpa}}(n)=1 \wedge \lnot\mathsf{Repeat} \Big] \\ & \le \mathrm{Pr} \big[ \mathsf{Repeat} \big] + \mathrm{Pr} \Big[ \mathsf{PrivK}_{\mathcal{A},\widetilde{\Pi}}^{\mathsf{cpa}}(n)=1 \big | \lnot\mathsf{Repeat} \Big] \\ & \le \frac{q(n)}{2^n}+\frac{1}{2} \end{align} \]

即得到\((3)\)的结果。从上面的分析可知，该方案安全性的关键在于，避免生成挑战密文\(c\)时所用到的随机值\(r_c\)在加密预言机回答敌手询问时被使用，但即使是重复使用了，概率也是可以忽略的。

定义函数 \[ \varepsilon(n) \overset{\mathrm{def}}{=} \mathrm{Pr} \Big[ \mathsf{PrivK}_{\mathcal{A},\Pi}^{\mathsf{cpa}}(n)=1 \Big] - \frac{1}{2} \tag{4} \] 根据\(\varepsilon\)的定义，\(\mathcal{A}\)攻破\(\Pi\)的概率可表示为 \[ \mathrm{Pr} \Big[ \mathsf{PrivK}_{\mathcal{A},\Pi}^{\mathsf{cpa}}(n)=1 \Big] = \frac{1}{2} + \varepsilon(n) \tag{5} \] 只有当\(\varepsilon(n)\)为可忽略函数时，方案\(\Pi\)才是安全的。

归约证明

构造区分器\(\mathcal{D}\)，它将\(\mathcal{A}\)当作子程序运行。\(\mathcal{D}\)访问使用某函数的预言机\(\mathcal{O}\)，要判断该函数是「伪随机的」（即\(F_k, k\gets\{0,1\}^n\)）还是「随机的」（即\(f\gets\mathsf{Func}_n\)）。\(\mathcal{D}\)模拟\(\mathcal{A}\)的不可区分性实验，观察\(\mathcal{A}\)成功与否，以确定\(\mathcal{O}\)使用的是伪随机函数还是随机函数。

向\(\mathcal{D}\)输入\(1^n\)和可访问的预言机\(\mathcal{O}\)，让\(\mathcal{A}\)执行CPA不可区分实验：

\(\mathcal{A}\)可以访问\(\mathcal{O}\)，对\(\mathcal{A}\)输入\(1^n\)，\(\mathcal{A}\)输出一对长度相等的消息\(m_0\)和\(m_1\)
随机选择\(b\gets\{0,1\}\)，均匀随机选择\(r\gets\{0,1\}^n\)，向\(\mathcal{O}\)询问得到\(s'\gets\mathcal{O}(r)\)，将\(c:=\left \langle r,s'\oplus m_b \right \rangle\)交给\(\mathcal{A}\)
\(\mathcal{A}\)继续访问\(\mathcal{O}\)，\(\mathcal{O}\)继续回答\(\mathcal{A}\)的询问，\(\mathcal{A}\)最终输出一个比特\(b'\)
如果\(b=b'\)，则该实验输出\(1\)，否则输出\(0\)

那么，\(\mathcal{A}\)作为\(\mathcal{D}\)的子程序运行时的视图与\(\mathcal{A}\)攻击加密方案时的视图相同，而且过程完全一样。\(\mathcal{O}\)使用伪随机函数\(F_k\)与加密方案\(\Pi\)对应，\(\mathcal{O}\)使用随机函数\(f\)与加密方案\(\widetilde{\Pi}\)对应，所以 \[ \mathrm{Pr} \big[ D^{F_k(\cdot)}(1^n)=1 \big] = \mathrm{Pr} \Big[ \mathsf{PrivK}_{\mathcal{A},\Pi}^{\mathsf{cpa}}(n)=1 \Big] \tag{6} \] \[ \mathrm{Pr} \big[ D^{f(\cdot)}(1^n)=1 \big] = \mathrm{Pr} \Big[ \mathsf{PrivK}_{\mathcal{A},\widetilde{\Pi}}^{\mathsf{cpa}}(n)=1 \Big] \tag{7} \] 综合\((3)\)、\((5)\)、\((6)\)、\((7)\)可得 \[ \mathrm{Pr} \big[ D^{F_k(\cdot)}(1^n)=1 \big] - \mathrm{Pr} \big[ D^{f(\cdot)}(1^n)=1 \big] \ge \varepsilon(n) - \frac{q(n)}{2^n} \tag{8} \]

有了上面的结果，构造归约证明，过程如下：

指定敌手\(\mathcal{A}\)攻击方案\(\Pi\)，成功的概率与\(1/2\)的差值为\(\varepsilon(n)\)
假设：问题\(\mathsf{X}\)难以解决，无法在概率多项式时间内以不可忽略的概率区分\(F_k\)和\(f\)
归约：构造区分器\(\mathcal{D}\)，它将\(\mathcal{A}\)当作子程序运行，执行CPA不可区分实验，可得到结论 \[ \mathrm{Pr} \big[ D^{F_k(\cdot)}(1^n)=1 \big] - \mathrm{Pr} \big[ D^{f(\cdot)}(1^n)=1 \big] \ge \varepsilon(n) - \frac{q(n)}{2^n} \]
矛盾：若\(\varepsilon(n)\)不可忽略，则上面得到的概率也不可忽略，这与假设相矛盾
结论：\(\mathcal{A}\)无法以不可忽略的概率攻破方案\(\Pi\)，方案\(\Pi\)是CPA安全的