密码学中的归约证明过程
证明过程
归约证明(proof by reduction)是现代密码学中证明方案安全性的重要方法,甚至是一些教材中使用的唯一方法。它的思路是,假设某个问题难以解决,然后证明基于该问题的构造方法在该假设下是安全的。
想要证明某构造方案\(\Pi\)安全,假设已知问题\(\mathsf{X}\)难以解决,将成功攻破该方案\(\Pi\)的有效敌手\(\mathcal{A}\)转化为成功解决问题\(\mathsf{X}\)的有效算法\(\mathcal{A}'\),这与假设相矛盾,所以方案\(\Pi\)无法攻破,方案是安全的。具体过程如下:
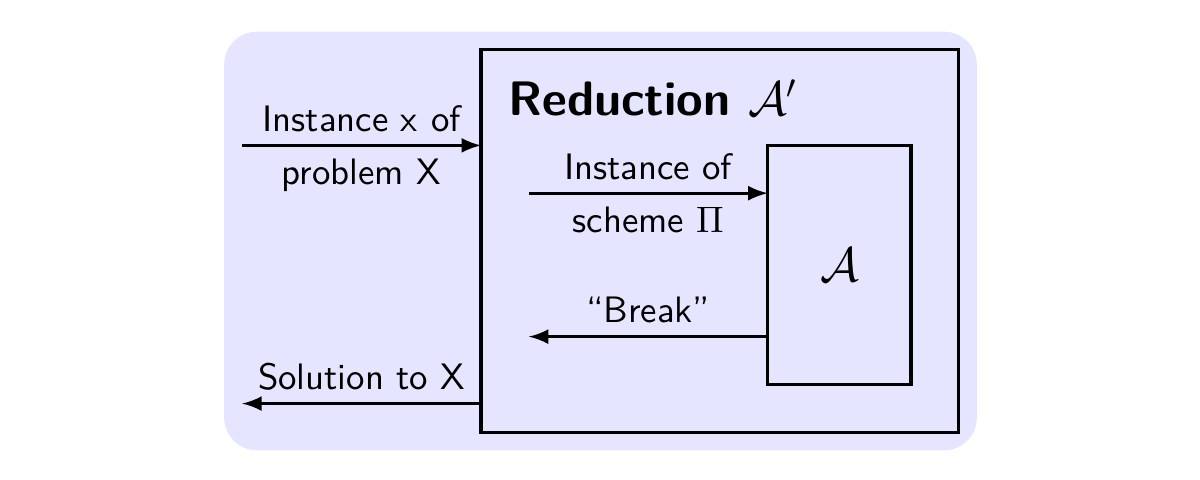
- 指定概率多项式时间的敌手\(\mathcal{A}\)攻击方案\(\Pi\),成功的概率为\(\varepsilon(n)\)
- 假设:问题\(\mathsf{X}\)难以解决,即无法在概率多项式时间内以不可忽略的概率解决
- 归约:构造有效算法\(\mathcal{A}'\),它将\(\mathcal{A}\)当作子程序运行,从问题\(\mathsf{X}\)的实例\(\mathsf{x}\)模拟出一个\(\Pi\)的实例,输入给\(\mathcal{A}\),如果\(\mathcal{A}\)成功攻破,则\(\mathcal{A}'\)成功解决实例\(\mathsf{x}\)的概率至少为多项式的倒数\(1/p(n)\)
- 矛盾:那么\(\mathcal{A}'\)解决问题\(\mathsf{X}\)的概率为\(\varepsilon(n)/p(n)\),若\(\varepsilon(n)\)不可忽略,则\(\varepsilon(n)/p(n)\)也不可忽略,这与假设相矛盾
- 结论:敌手\(\mathcal{A}\)无法以不可忽略的概率攻破方案\(\Pi\),或者说\(\Pi\)是计算安全的
第3步归约中的概率\(1/p(n)\)我是这么理解的,它表示从\(\mathcal{A}'\)的输入到\(\mathcal{A}\)的输入以及从\(\mathcal{A}\)的输出到\(\mathcal{A}'\)的输出这两个交互过程成功的概率。只有整个过程全部成功,才认为\(\mathcal{A}'\)成功解决问题的实例\(\mathsf{x}\),总的概率为\(1/p(n)\)乘以\(\mathcal{A}\)攻破\(\Pi\)的概率\(\varepsilon(n)\)。
简单的证明例子
伪随机数发生器(pseudorandom generator, PRG)输入长度为\(n\)的种子\(s\),算法\(G\)输出长度为\(l(n)\)的字符串。满足\(l(n)>n\)称为扩展性,即用短的种子生成长的字符串。无法区分它和均匀随机选择的字符串称为伪随机性,用数学语言描述就是,对于概率多项式时间的区分器\(\mathcal{D}\)来说,存在可忽略函数\(\mathsf{negl}\)满足: \[ \left| \mathrm{Pr}[D(r)=1] - \mathrm{Pr}[D(G(s))=1] \right| \le \mathsf{negl}(n) \] 其中\(r\)是从\(\left \{ 0,1 \right\}^{l(n)}\)中均匀随机选择的,种子\(s\)是从\(\left \{ 0,1 \right\}^{n}\)中均匀随机选择的。
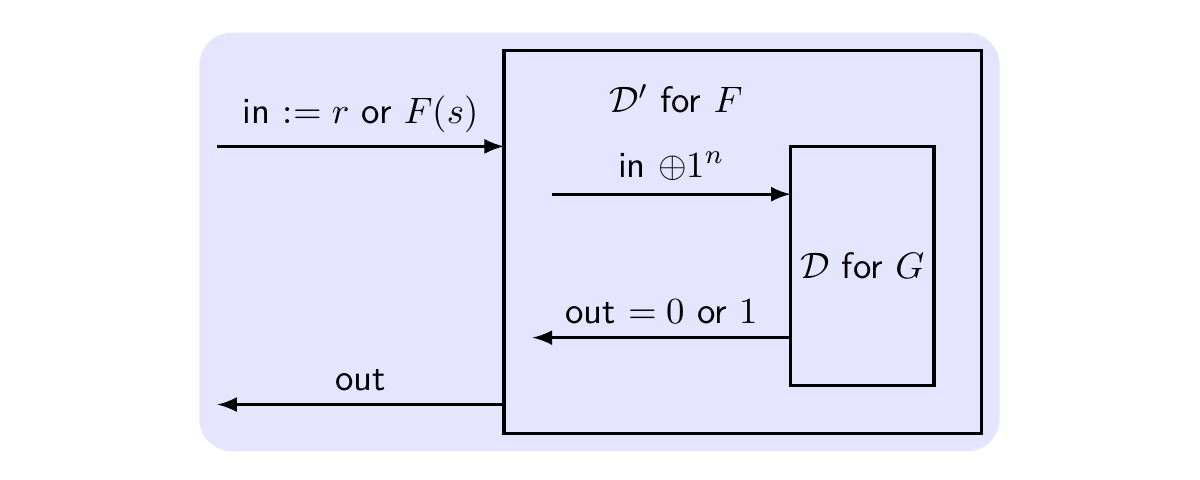
我们用归约方法证明:如果\(F(s)\)是伪随机数发生器,则\(G(s)=F(s)\oplus 1^n\)也是。关键在于将证明\(G(s)\)的伪随机性转化为证明\(F(s)\)的伪随机性,过程如下:
- 指定概率多项式时间的区分器\(\mathcal{D}\),\(\mathcal{D}\)成功区分\(G(s)\)和\(r\)的概率 \[ \varepsilon(n) = \mathrm{Pr}[D(r)=1] - \mathrm{Pr}[D(G(s))=1] \]
- 假设:问题\(\mathsf{X}\)难以解决,即成功区分\(F(s)\)和\(r\)的概率可忽略
- 归约:构造算法\(\mathcal{D}'\)区分\(F(s)\)和\(r\),\(\mathcal{D}'\)将\(\mathcal{D}\)作为子程序运行,计算\(\mathcal{D}'\)成功区分的概率 \[ \begin{align} \mathrm{Pr}[D'(r)=1] - \mathrm{Pr}[D'(F(s))=1] & = \mathrm{Pr}[D(r\oplus 1^n)=1] - \mathrm{Pr}[D(F(s)\oplus 1^n)=1] \\ & = \mathrm{Pr}[D(r)=1] - \mathrm{Pr}[D(G(s))=1] \\ & = \varepsilon(n) \end{align} \]
- 矛盾:若\(\mathcal{D}'\)成功区分\(F(s)\)和\(r\)的概率\(\varepsilon(n)\)不可忽略,则与假设矛盾
- 结论:\(\mathcal{D}\)无法以不可忽略的概率区分\(G(s)\)和\(r\),\(G(s)\)也是伪随机数发生器,得证
上面的例子中\(1/p(n)\)的值为\(1\),可以认为\(\mathcal{D}'\)与\(\mathcal{D}\)的交互过程非常「顺利」。
经典算法对应的基础问题
通过归约可将要证明的结论等价为更基础的问题,上面的例子将\(G(s)\)的伪随机性等价为\(F(s)\)的伪随机性。类似地,很多密码方案的安全性可以等价为一些基础问题的困难性。比如,RSA算法之所以安全是因为大整数质因数分解很困难,ElGamal算法之所以安全是因为离散对数求解困难。所以,在证明方案的安全性时,可将安全性证明归约到求解基础问题的困难性上。