LMI基础及YALMIP求解实例

发表于 分类于 Waline： 本文字数： 1.4k 阅读时长 ≈ 5 分钟

教材

最近通过阅读段广仁院士的英文著作LMIs in Control Systems学习线性矩阵不等式（Linear Matrix Inequality, LMI），本文是第一章主要内容的总结，还附带了一个用YALMIP求解LMI问题的例子。

网上有作者当年在哈工大的授课视频，课程名为控制系统设计的线性矩阵不等式方法，段院士讲课很好，体现了深厚的数学和控制理论功底。国外还有门MAE 509: LMI Methods in Optimal and Robust Control课程，教材就选的这本书，但我觉得这个老外讲课一般，主要是声音忽高忽低，时而听不清时而炸耳朵，不过他的课件做得还不错。

LMI的定义

从线性矩阵不等式这个名字就知道，LMI是关于矩阵的不等式，而且关于矩阵变量是线性的。它的标准形式定义如下：

LMI标准形式的定义

很多常见的矩阵不等式都可以化成标准形式。

典型问题转化为LMI问题

线性代数中很多典型问题都可以转化为LMI问题，比如下面的特征值最小化（eigenvalue minimization）问题

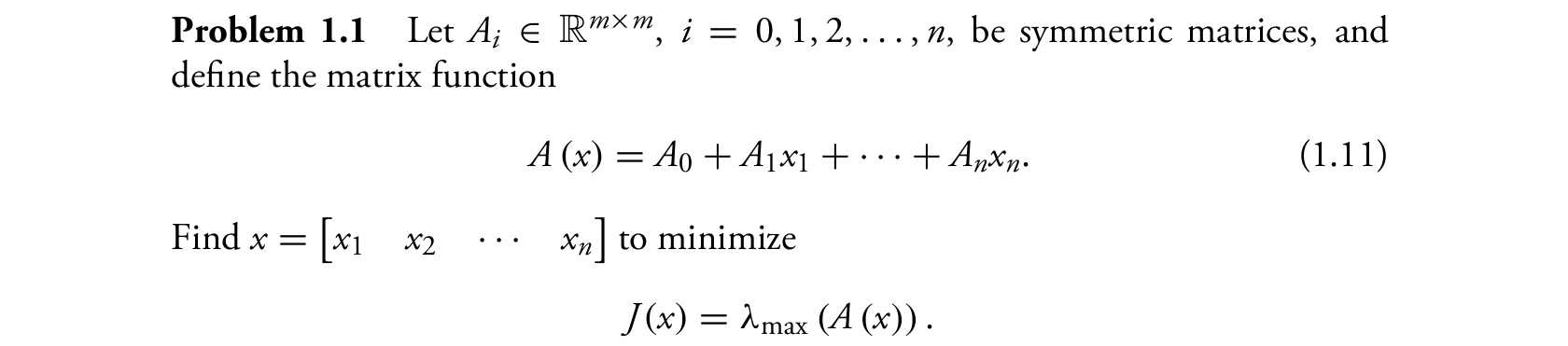
特征值最小化问题

可以转化为如下LMI问题

与其等价的LMI问题

很明显，矩阵不等式约束关于参数\(x_i,\,i=1,2,\dots,n\)和\(t>0\)是线性的。矩阵的特征值是这些参数的函数，当矩阵特别大时，求解该问题非常复杂。现在已经有非常成熟的LMI求解工具，接下来介绍如何在MATLAB中利用YALMIP工具箱求解该LMI问题。

求解工具YALMIP

安装注意事项

YALMIP的安装过程可参考Installation - YALMIP。还需要选择和安装合适的求解器，我选用的是mosek，可求解YALMIP支持的大部分问题，mosek是商业软件，学术用途是免费的，需要申请免费许可。

YALMIP和mosek安装好后，在MATLAB中运行yalmiptest命令测试功能，在我的机器上，只有Nonlinear SDP (NLSDP)问题的测试没有通过。SDP是semidefinite programming的缩写，不过我应该没有求解非线性SDP问题的需求。包括LMI在内的很多优化问题最后要判断矩阵的正定性，所以SDP问题非常重要。

求解过程

为了验证结果是否正确，我用YALMIP求解这篇论文中的例子，并与论文给出的结果做对比。对照上述等价LMI问题的描述，基于Getting started - YALMIP中提供的模板，编写如下代码求解特征值最小化问题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
%% 先准备好问题要用到的数据
% 一共有6个5x5的对称矩阵
A0 = [-0.69 -0.32  0.34  0.43 -0.05;
      -0.32 -0.11 -0.11 -0.45 -0.34;
       0.34 -0.11 -0.71 -0.33 -0.08;
       0.43 -0.45 -0.33  0.65  0.27;
      -0.05 -0.34 -0.08  0.27  0.39];
A1 = [-0.66  0.31  0.57 -0.06 -0.44;
       0.31 -0.23 -0.12 -0.35  0.28;
       0.57 -0.12 -0.26 -0.06 -0.37;
      -0.06 -0.35 -0.06  0.64  0.34;
      -0.44  0.28 -0.37  0.34  0.61];
A2 = [-0.31  0.35  0.06 -0.23  0.17; 
       0.35  0.24 -0.19  0.21 -0.12;
       0.06 -0.19 -0.34  0.00 -0.36;
      -0.23  0.21  0.00  0.16 -0.24;
       0.17 -0.12 -0.36 -0.24  0.00];
A3 = [ 0.27 -0.14  0.13 -0.32 -0.08;
      -0.14 -0.20 -0.29 -0.05 -0.64;
       0.13 -0.29 -0.45 -0.20 -0.59;
      -0.32 -0.05 -0.20 -0.27 -0.46;
      -0.08 -0.64 -0.59 -0.46 -0.39];
A4 = [-0.57 -0.38 -0.09  0.31  0.22;
      -0.38  0.66  0.17 -0.03  0.51;
      -0.09  0.17  0.23  0.12 -0.21;
       0.31 -0.03  0.12 -0.56 -0.21;
       0.22  0.51 -0.21 -0.21  0.59];
A5 = [ 0.22  0.28  0.14  0.03  0.09;
       0.28  0.69 -0.12  0.10  0.30;
       0.14 -0.12 -0.77 -0.21  0.13;
       0.03  0.10 -0.21 -0.42 -0.15;
       0.09  0.30  0.13 -0.15  0.22];

% A(x)是6个矩阵的线性组合
Ax = A0 + x(1)*A1 + x(2)*A2 + x(3)*A3 + x(4)*A4 + x(5)*A5;


%% 求解LMI问题的标准代码现在开始
% 每次运行之前清理内部数据库
yalmip('clear')

% 定义变量，x是满足约束条件的参数变量，t是得到的最大特征值
x = sdpvar(5, 1);
t = sdpvar(1);

% 约束条件
Constraints = [Ax - t*eye(5) <= 0];

% 目标函数
Objective = t;

% 选项配置，可自定义求解器，否则会自动指定
options = sdpsettings('verbose', 1);

% 求解最优化问题
sol = optimize(Constraints, Objective, options);

% 输出控制
if sol.problem == 0
    solution = value(x);
    min_eigen = value(t);
else
    disp('Hmm, something went wrong!');
    sol.info
    yalmiperror(sol.problem)
end

YALMIP计算得到的解与对应的最小特征值分别为

1
2
3
4
5
6
7
8
9
10
11
solution =

  -0.6136
   0.6145
  -0.3437
  -0.6068
   0.6465

min_eigen =

0.7089

该结果与论文中的完全一样，而且计算速度还挺快。读者可以基于上面代码修改，试着求解教材上提及的矩阵范数最小化问题以及线性系统的稳定性判定问题。

使用YALMIP的注意事项在Getting started - YALMIP中有介绍，比如YALMIP不支持严格不等式（约束条件不能为严格的不等号）、sdpvar定义的矩阵变量默认是对称矩阵等等，在使用前要认真阅读。

LMI的优势

LMI构造的是凸约束条件（convex constraints），因此很多涉及到LMI的都是凸优化（convex optimization）问题，所以一定有全局最优解。即使问题规模很大，也可以通过数值方法高效而可靠地（numerically efficiently and reliablly）求解。

很多控制理论的基本问题都可以转化为求解LMI问题，所以LMI在控制理论中的地位非常高，正如Doyle指出：

LMIs play the same central role in the postmodern theory as Lyapunov and Riccati equations played in the modern, and in turn various graphical techniques such as Bode, Nyquist and Nichols plots played in the classical.

所以，上世纪90年代以来，LMI一直是控制领域写（shui）论文的利器，这正是我学习它的原因。希望这个暑假，或者今年，我也能用LMI投一篇论文，缓解下一直以来我那颗狂躁不安的心。