系统的输入输出稳定性
简介
与状态空间模型不同,输入输出模型直接将系统的输入和输出联系起来,而无需通过状态方程描述内部结构,通常将系统视为一个黑箱。输入输出稳定性关注输入与输出之间的关系,而Lyapunov稳定性则着重于系统状态的演变。
\(\mathcal{L}\)稳定性
考虑输入输出关系由如下方程描述的系统 \[ y=Hu \]
其中,\(H\)是一个映射或者算子。输入\(u\)属于一个信号空间,该信号空间中的信号是个函数\(u:\left[0,\infty\right)\to R^m\),将时间区间\(\left[0,\infty\right)\)映射到欧氏空间\(R^m\)。引入范数\(\lVert u \rVert\)来描述信号的大小。接着便为\(\mathcal{L}_{\infty}\)、\(\mathcal{L}_2\)和\(\mathcal{L}_p\)函数空间定义范数。为了与\(u\)作为\(R^m\)中向量的范数\(\lVert u \rVert\)区别开来,用\(\lVert u \rVert_{\mathcal{L}}\)表示\(u\)作为函数空间\(\mathcal{L}\)中函数的范数。\(\lVert u \rVert_{\mathcal{L}}\)的定义基于\(\lVert u \rVert\),但要将它们与\(u\)在欧氏空间中的几种范数\(\lVert u \rVert_{\infty}\)、\(\lVert u \rVert_2\)、\(\lVert u \rVert_p\)区别开来。

按照上述记号规则,可以将\(H\)定义为从\(\mathcal{L}^m\)到\(\mathcal{L}^q\)的映射。但这种定义方式并不合适,因为需要考虑不稳定系统。对于不稳定系统,输入\(u\in\mathcal{L}^m\)可能导致输出\(y\)不属于\(\mathcal{L}^q\)。因此,\(H\)通常定义为从扩展空间\(\mathcal{L}_e^m\)到扩展空间\(\mathcal{L}_e^q\)的映射,扩展空间定义为 \[ \mathcal{L}_e^m=\left\{u|u_{\tau}\in\mathcal{L}^m,\forall\tau\in\left[0,\infty\right)\right\} \] 其中,\(u_{\tau}\)是\(u\)的截断函数,定义为 \[ u_{\tau}(t) = \begin{cases} u(t), & 0\le t \le \tau \\ 0, & t>\tau \end{cases} \]
这种截断方式要求\(\mathcal{L}_e^m\)空间中的函数,即使在无限时域上可能无界,也必须在每个有限时间段内表现得如同\(\mathcal{L}^m\)空间中的函数一样。因此,\(\mathcal{L}^m\)是\(\mathcal{L}_e^m\)的子集。
映射\(H:\mathcal{L}_e^m\to\mathcal{L}_e^q\)被称为因果映射,如果在任意时间\(t\)的输出\((Hu)(t)\)只依赖于输入在\(t\)时刻及之前的值。因果性(causality)是由状态空间模型表示的动态系统的内在特性,它的定义等价于 \[ (Hu)_{\tau}=(Hu_{\tau})_{\tau} \]
有了输入输出信号空间的定义,便可以定义输入输出稳定性(input-output stability)。

对于\(\mathcal{L}\)稳定的因果系统,可推得\(u\in\mathcal{L}^m\Rightarrow Hu\in\mathcal{L}^q\),即输入\(u\)属于\(\mathcal{L}\)空间,则输出\(y\)也属于\(\mathcal{L}\)空间。而有限增益\(\mathcal{L}\)稳定性不仅要求输出在\(\mathcal{L}\)空间内,还对输入信号增益有限制。
在讨论不同类型的函数空间(\(\mathcal{L}_{\infty}\)、\(\mathcal{L}_2\)和\(\mathcal{L}_p\))时,有不同的\(\mathcal{L}\)稳定性定义,如\(\mathcal{L}_{\infty}\)稳定性和\(\mathcal{L}_2\)稳定性,这是由于不同函数空间中的信号特征不同。以\(\mathcal{L}_{\infty}\)空间为例,该空间包含按段光滑有界函数,因此\(\mathcal{L}_{\infty}\)稳定性对应于我们熟悉的有界输入有界输出稳定性(bounded-input-bounded-output stability)的概念。
上述定义要求不等式\((6.1)(6.2)\)对输入空间\(\mathcal{L}^m\)中的所有信号都成立。对于很多实际系统,输入输出之间的关系只定义在输入空间的一个子集上。于是便催生出了小信号\(\mathcal{L}\)稳定性的概念:
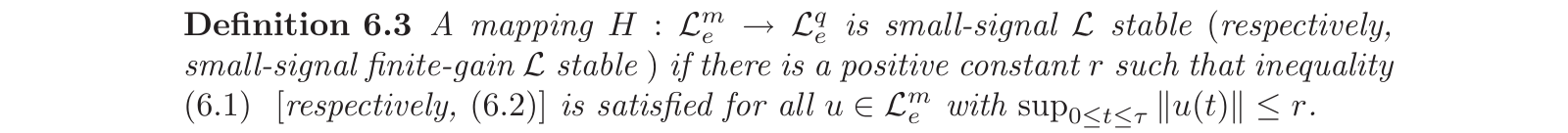
小信号\(\mathcal{L}\)稳定性更适合用于分析系统在特定工作点的行为,而\(\mathcal{L}\)稳定性则更适合于分析系统整体或在整个工作范围内的行为。
状态空间模型的\(\mathcal{L}\)稳定性
Lyapunov稳定性侧重于研究平衡点的稳定性以及状态的渐进特性。接下来探讨如何利用Lyapunov稳定性分析工具来建立由状态空间模型表示的非线性系统的\(\mathcal{L}\)稳定性。系统状态空间模型为 \[ \dot{x}=f(x,u),\,y=h(x,u) \]
\(\mathcal{L}_{\infty}\)稳定性定理体现了与输入到状态稳定(input-to-state stability)的关系:

小信号\(\mathcal{L}_{\infty}\)稳定性定理体现了与渐进稳定(asymptotically stability)的关系:
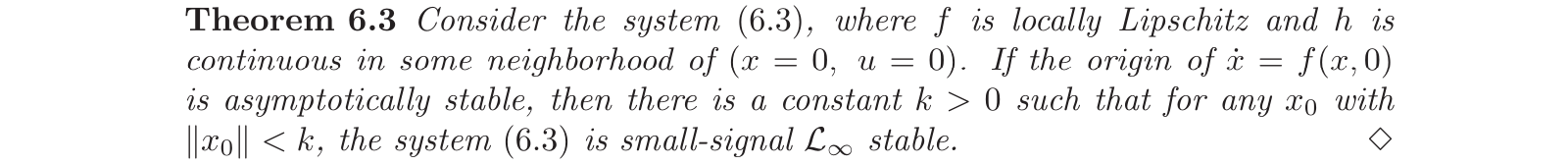
\(\mathcal{L}_2\)增益
\(\mathcal{L}_2\)稳定性是系统分析中非常重要的概念。因为平方可积信号可以视为能量有限的信号,在实际中很常见。在很多控制问题中,例如\(H_{\infty}\)控制,系统表示为输入到输出的映射,并希望这个映射尽可能小。对于\(\mathcal{L}_2\)输入信号,要确保系统输入到输出映射是有限增益\(\mathcal{L}_2\)稳定,而且努力使\(\mathcal{L}_2\)增益达到最小。分析这些问题时,不仅要能够判断系统是有限增益\(\mathcal{L}_2\)稳定的,而且还要计算出\(\mathcal{L}_2\)增益或者它的上限。
对于线性系统,有如下结论:
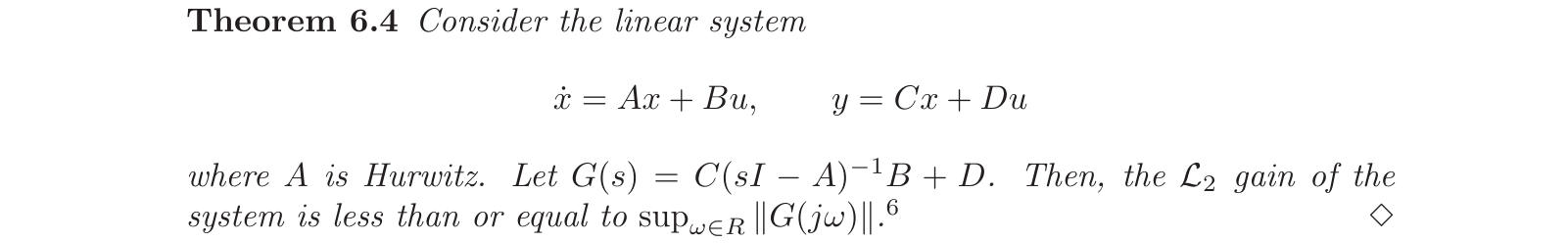
从上述定理可知,\(\sup_{\omega\in R}\lVert G(j\omega) \rVert\)就是\(\mathcal{L}_2\)增益,而且它就是\(G(j\omega)\)的\(H_{\infty}\)范数。
对于非线性系统,有两个结论。第一个结论与系统的无源性有关:

第二个结论则与\((6.20)\)所示的Hamilton-Jacobi不等式有关:
